Mechanical Engineering graduated school project
Algorithm class - Dynamic time warping (2021-1)
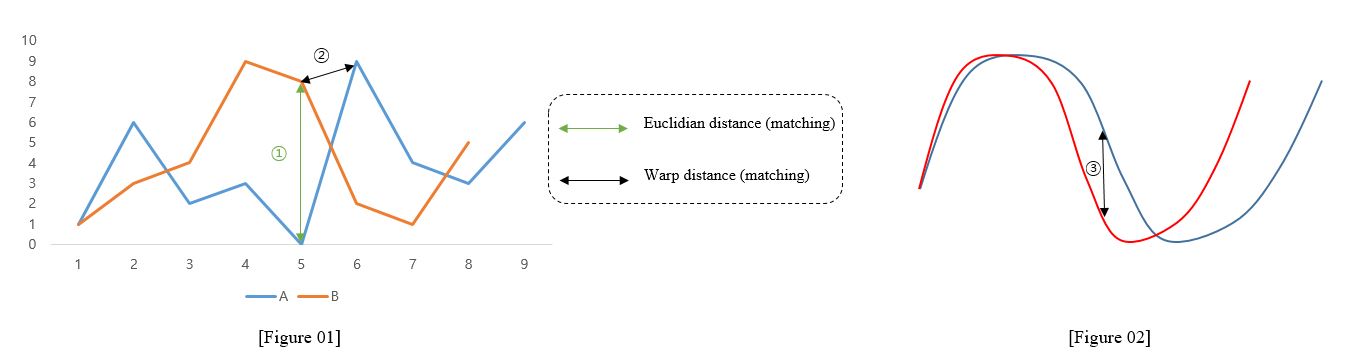
(a) measurment of similarity
To define similarity, numerous people have attempted to quantify the smallest distance between two number sequences. The most well-known quantitative metric of similarity is Euclidian Distance. However, the accuracy of measuring similarity between two sequences using solely vertical Euclidean distance matching might vary significantly. In any case Using warp distance matching, the real degree of similarity can be determined. In this method, the most similar point between two numerical sequences is identified, paired, and the distance between them is measured and expressed in a metric.
This algorithm utilizes dynamic programming.
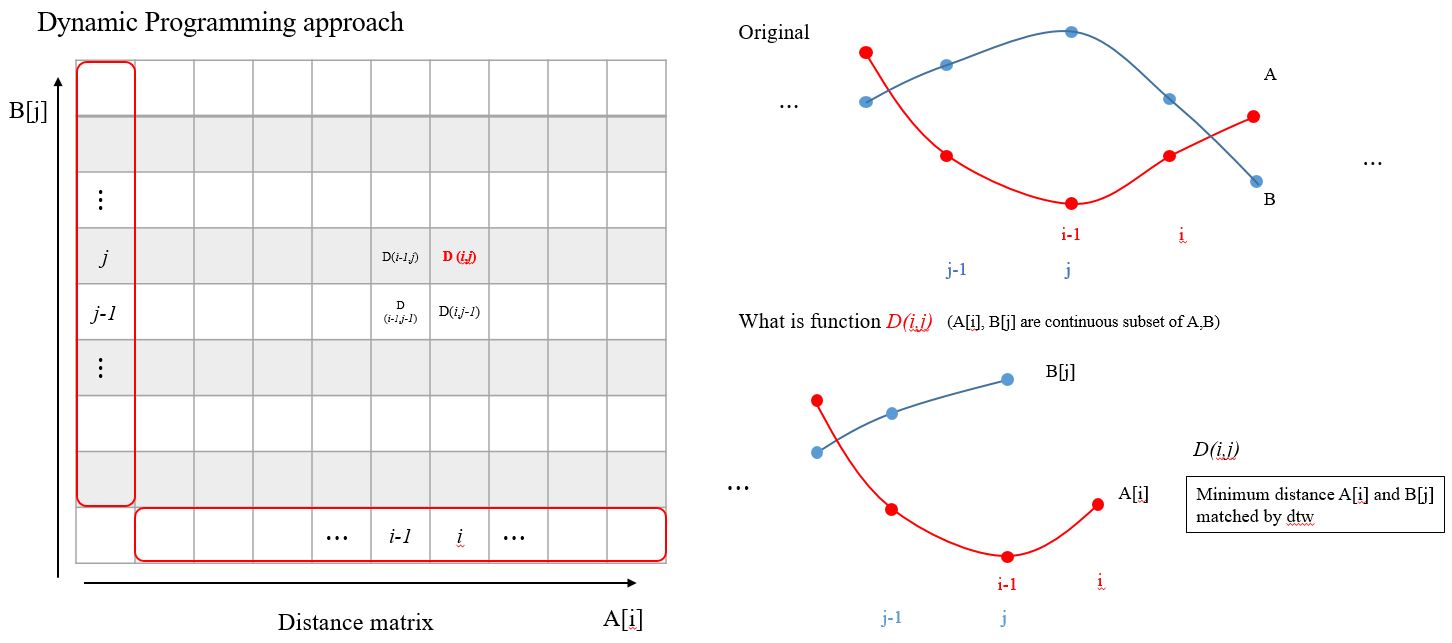
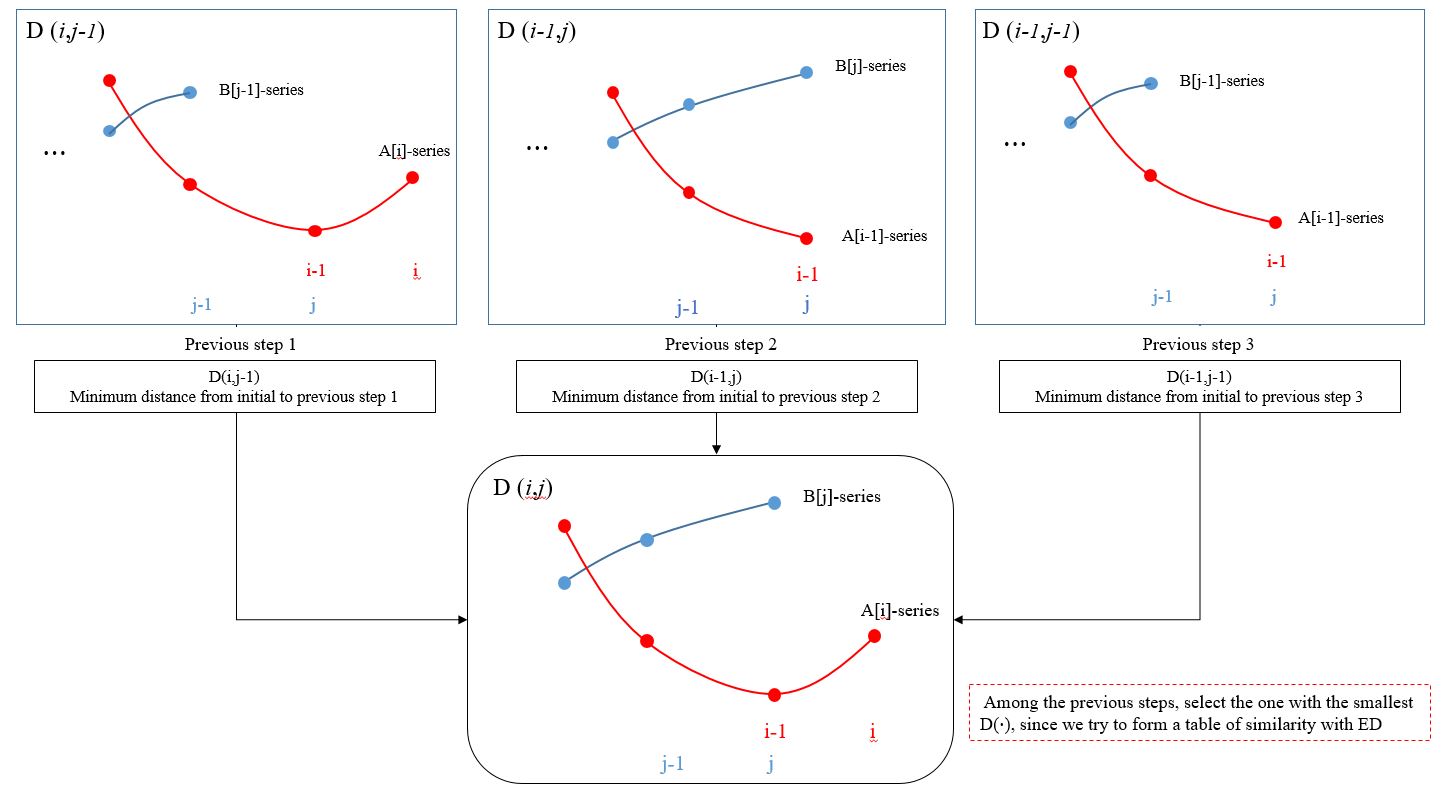
(b) DTW Algorithm
recursive relation formula is as follows.
$$ {D}(i,j) = \vert A_{i} - B{j}\vert + min \,[D(i, j-1),\; D(i-1, j-1), \; D(i-1, j)] -(1) $$
Capital D(i,j) is distance between A sequence point i and B seqeunce point j. and D(i-1,j-1), D(i-1,j), D(i, j-1) is previous steps of D(i,j).
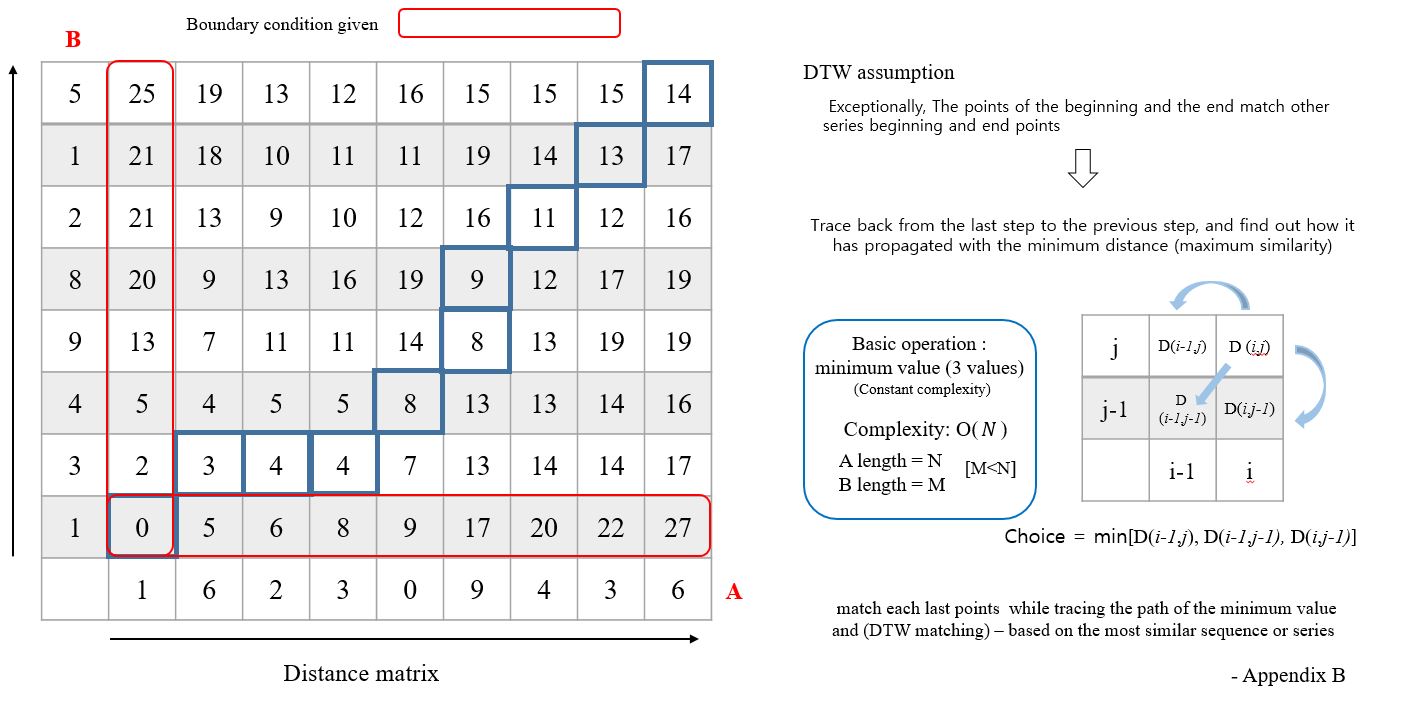
Given boundary conditions (values for tow sequences), populate your dynamic programming table using the aforementioned recursive algorithm. After completing the filling of your table, couple two points by backtracking your steps from the last point.
Description: Link to Notion